¿Que es?

En matemáticas, un conjunto es una colección de elementos con características similares considerada en sí misma como un objeto. Los elementos de unconjunto, pueden ser las siguientes: personas, números, colores, letras, figuras, etc. ... Un conjuntosuele definirse mediante una propiedad que todos sus elementos poseen. 

EJERCICIOS

1. es un conjunto. Los elementos que forman este conjunto son: 2, 4, 6

2. ¿Cuántos elementos hay en el conjunto ? 3 elementos

3. A= B =  

 ¿4 es un elemento de A? No

 ¿4 es un elemento de B? Si

4. Si U = , entonces 7 ∉ U,

 ¿Se podría extraer A= de este universo? No 

¿Se podría extraer B = ? Si 

5. A=   B =

 ¿8 ∈ A? No

 ¿8 ∈ B? Si 

6. Del ejemplo anterior como 8 no es un miembro de A podemos escribir: 8 ∉ A 

 7. A= 1,2,3 , B= 1,5,2,7 { } { } 

¿Se cumple x A xB ∈ →∈ ? SI 

¿Se cumple xB xA ∈ →∈ ? NO ¿Son iguales los dos conjuntos? NO 

8. C= 6,4 { } Escribe un conjunto D tal que D=C D = 4,6 { }

 9. Si U = , B = y C = , entonces el conjunto formado por todos los elementos comunes a B y C se le llama conjunto vació.

 10. Si P = , P también es finito aunque sea difícil contar los ríos del Mundo. 11. El conjunto de números que son múltiplos de 5 es un conjunto infinito porque no nunca se llega a un fin , observa: A 5,10,15, 0 ...... = { 2 , } 

Tipos

Las clases de conjuntos se pueden clasificar en iguales, finitos e infinitos, subcojuntos, vacíos, disjuntos o disyuntivos, equivalentes, unitarios, superpuestos o solapados, congruentes y no congruentes, entre otros. 

1- Conjuntos iguales

Dos conjuntos son iguales si tienen exactamente los mismos elementos.

Por ejemplo:

• Si A = {Vocales del alfabeto} y B = {a, e, i, o, u} se dice que A = B.
• Por otro lado, los conjuntos {1, 3, 5} y {1, 2, 3} no son iguales, porque tienen diferentes elementos. Esto se escribe como {1, 3, 5} ≠ {1, 2, 3}.
• El orden en que los elementos están escritos dentro los corchetes no importa en absoluto. Por ejemplo, {1, 3, 5, 7, 9} = {3, 9, 7, 5, 1} = {5, 9, 1, 3, 7}.
• Si un elemento aparece en la lista más de una vez, sólo se contabiliza una vez. Por ejemplo, {a, a, b} = {a, b}.

El conjunto {a, a, b} tiene sólo los dos elementos a y b. La segunda mención de a es una repetición innecesaria y puede ser ignorada. Normalmente se considera mala notación cuando se enumera a un elemento más de una vez.

2- Conjuntos finitos e infinitos

Los conjuntos finitos, son aquellos en donde pueden ser contabilizados o enumerados todos elementos del conjunto. Aquí hay dos ejemplos:

• {Números enteros entre 2.000 y 2.005} = {2.001, 2.002, 2.003, 2.004}
• {Números enteros entre 2.000 y 3.000} = {2.001, 2.002, 2.003, ..., 2.999}

Los tres puntos '...' en el segundo ejemplo representan los otros 995 números en el conjunto. Se pudo haber listado a todos los elementos, pero para ahorrar espacio se utilizaron puntos en su lugar. Esta notación sólo puede utilizarse si está completamente claro lo que significa, como en esta situación.

Un conjunto también puede ser infinito - lo único que importa es que esté bien definido. Aquí hay dos ejemplos de conjuntos infinitos:

• {Números pares y enteros mayores o iguales a dos} = { 2, 4, 6, 8, 10, ...}
• {Números enteros mayores que 2.000} = {2.001, 2.002, 2.003, 2.004, ...}

Ambos conjuntos son infinitos, ya que no importa cuántos elementos se intente enumerar, siempre hay más elementos en el conjunto que no podrán ser listados, no importa cuánto tiempo se pruebe. Esta vez los puntos '...' tienen un significado ligeramente diferente, porque representan infinitamente muchos elementos no enumerados.

3- Conjuntos subconjuntos

Un subconjunto es una parte de un conjunto.

• Ejemplo: Los búhos son un tipo particular de aves, así que cada búho es también un ave. En el lenguaje de los conjuntos, se expresa diciendo que el conjunto de búhos es un subconjunto del conjunto de las aves.

Un conjunto S es llamado un subconjunto de otro conjunto T, si cada elemento de S es un elemento de T. Esto se escribe como:

• S ⊂ T (Se lee "S es un subconjunto de T")

El nuevo símbolo ⊂ significa 'es un subconjunto de'. Así {búhos} ⊂ {pájaros} porque cada búho es un pájaro.

• Si A = {2, 4, 6} y B = {0, 1, 2, 3, 4, 5, 6}, entonces A ⊂ B,

Porque cada elemento de A es un elemento de B.

El símbolo ⊄ quiere decir 'no es un subconjunto'.

Esto significa que al menos un elemento de S no es un elemento de T. Por ejemplo:

• {Aves} ⊄ {criaturas voladoras}

Porque un avestruz es un ave, pero no vuela.

• Si A = {0, 1, 2, 3, 4} y B = {2, 3, 4, 5, 6}, entonces A ⊄

Porque 0 ∈ A, pero 0 ∉ B, se lee "0 pertenece al conjunto A", pero "0 no pertenece al conjunto B".

4- Conjunto vacío

El símbolo Ø representa el conjunto vacío, que es el conjunto que no tiene elementos en absoluto. Nada en el universo entero es un elemento de Ø:

• | Ø | = 0 y X ∉ Ø, no importa lo que X puede ser.

Sólo hay un conjunto vacío, porque dos conjuntos vacíos tienen exactamente los mismos elementos, por lo que deben ser iguales entre sí.

5- Conjuntos disjuntos o disyuntivos

Dos conjuntos se llaman disjuntos si no tienen elementos en común. Por ejemplo:

• Los conjuntos S = {2, 4, 6, 8} y T = {1, 3, 5, 7} son disjuntos.

6- Conjuntos equivalentes

Se dice que A y B son equivalentes si tienen la misma cantidad de elementos que los constituyen, es decir, el numero cardinal del conjunto A es igual al número cardinal del conjunto B, n (A) = n (B). El símbolo para denotar un conjunto equivalente es '↔'.

• Por ejemplo:
  A = {1, 2, 3}, por lo tanto, n (A) = 3
  B = {p, q, r} , por lo tanto, n (B) = 3
  Por lo tanto, A ↔ B

7- Conjuntos unitarios

Es un conjunto que tiene exactamente un elemento en él. En otras palabras, sólo hay un elemento que conforma el conjunto.

Por ejemplo:

• S = {a}
• Sea B = { es un número primo par}

Por lo tanto, B es un conjunto unitario porque sólo hay un número primo que es par, es decir, 2.

8- Conjunto universal o referencial

Un conjunto universal es la colección de todos los objetos en un contexto particular o teoría. Todos los demás conjuntos en ese marco constituyen subconjuntos del conjunto universal, que se denomina con la letra mayúscula y cursiva U.

La definición precisa de U depende del contexto o teoría bajo consideración. Por ejemplo:

• Se pude definir U como el conjunto de todas las cosas vivientes en el planeta Tierra. En ese caso, el conjunto de todos los felinos es un subconjunto de U, el conjunto de todos los peces es otro subconjunto de U.
• Si se define U como el conjunto de todos los animales en planeta tierra, entonces el conjunto de todos los felinos es un subconjunto de U, el conjunto de todos los peces es otro subconjunto de U, pero el conjunto de todos los árboles no es un subconjunto de U.

9- Conjuntos superpuestos o solapados

Dos conjuntos que tienen al menos un elemento común se llaman conjuntos superpuestos.

• Ejemplo: Sean X = {1, 2, 3} e Y = {3, 4, 5}

Los dos conjuntos X e Y tienen un elemento en común, el número 3. Por lo tanto, se llaman conjuntos superpuestos.

10- Conjuntos Congruentes.

Son aquellos conjuntos en los que cada elemento de A tiene la misma relación de distancia con sus elementos imagen de B. Ejemplo:

• B { 2, 3, 4, 5, 6 } y A { 1, 2, 3, 4, 5 }

La distancia entre: 2 y 1, 3 y 2, 4 y 3, 5 y 4, 6 y 5 es una (1) unidad, por lo que A y B son conjuntos congruentes.

11- Conjuntos no congruentes

Son aquellos en los que no se puede establecer la misma relación de distancia entre cada elemento de A con su imagen en B. Ejemplo:

• B { 2, 8, 20, 100, 500 } y A { 1, 2, 3, 4, 5 }

La distancia entre: 2 y 1, 8 y 2, 20 y 3, 100 y 4, 500 y 5 es diferente, por lo que A y B son conjuntos no congruentes.

12- Conjuntos homogéneos

Todos los elementos que componen el conjunto pertenecen a la misma categoría, género o clase. Son del mismo tipo. Ejemplo:

• B { 2, 8, 20, 100, 500 }

Todos los elementos de B son número por lo que el conjunto se considera homogéneo.

13- Conjuntos heterogéneos

Los elementos que forman parte del conjunto pertenecen a diferentes categorías. Ejemplo:

• A { z, auto, π, edificios, manzana }

No existe una categoría a la que pertenezcan todos los elementos del conjunto, por lo tanto es un conjunto heterogéneo. 

¿Que es?

Se llama sucesión a un conjunto de números dados ordenadamente de modo que se puedan numerar: primero, segundo, tercero,.... Los elementos de la sucesión se llaman términos y se suelen designar mediante una letra con los subíndices correspondientes a los lugares que ocupan en la sucesión: a1, a2, a3, ... Por ejemplo, son sucesiones las siguientes listas de números: 1, 2, 3, 4, 5, ... 2, 4, 8, 16, 32, ... -3, 3, -3, 3, -3, ... En algunas ocasiones es posible expresar el término n-ésimo (término que ocupa el lugar n) en función de n. Este término se llama término general de la sucesión, y se simboliza con an. Por ejemplo, en la sucesión 1, 4, 9, 16, 25, ... cada término es el cuadrado del lugar que ocupa en la sucesión, con lo que el término general an = n². Cuando se conoce el término general de una sucesión se puede encontrar cualquier término. Por ejemplo, en la sucesión anterior, sabemos que el décimo término es 100, el que ocupa el lugar 20 es 20² = 400, el que ocupa el lugar 25 es 25² = 625, ... No todas las sucesiones tienen término general. Por ejemplo, la sucesión de los números primos: 2, 3, 5, 7, 11, 13, 17, ... En otras sucesiones, para hallar un término es necesario operar con dos o más de los anteriores y se llaman sucesiones recurrentes. Para hallar un término concreto hay que obtener, previamente, todos los anteriores. Por ejemplo, la sucesión de Fibonacci es una sucesión recurrente donde cada término se obtiene sumando los dos anteriores: 1, 1, 2, 3, 5, 8, 13, ...

Ejercicios

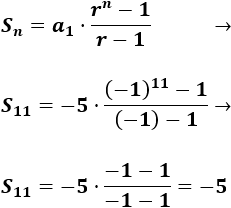
Problema 1

En una progresión aritmética, sabemos que el sexto término es 28 y que la diferencia es 5. Calcular el término general y los 5 primeros términos.

Problema 2

En una progresión geométrica, sabemos que el primer término es 6 y el cuarto 48. Calcular el término general y la suma de los 5 primeros términos.

Problema 3

Encontrar el término general de la sucesión

20, 19.3, 18.6, 17.9, ...

¿Es aritmética o geométrica? Encontrar los términos: décimo (10), vigésimo (20) y trigésimo (30).

Problema 4

Encontrar el término general de la sucesión

0.5, 0.25, 0.125, 0.0625,...

¿Es aritmética o geométrica? Calcular los términos n- ésimos para los valores de n = 10, 100.

Se sabe que la suma de los infinitos términos de esta sucesión es 1 (ejercicio 26). Razonar cómo es posible que la suma de infinitos términos positivos no sea infinita.

Problema 5

En una progresión aritmética, sabemos que el primer término es 1 y la suma de los 10 primeros términos es 63. Calcular el término general.

Tipos de sucesiones:

• Sucesión finita: es una sucesión, una serie de elementos que tienen un final. El primer y último número ya están definidos.
• Sucesión infinita: son aquellas sucesiones que no tienen un final y siempre se distinguen por ir seguido de los tres puntos (...).

Una vez entendida esta clasificación de sucesiones algebraicas más general, profundizamos en los distintos tipos de sucesiones matemáticas definiendo cada una:

1. Sucesiones convergentes

Este tipo corresponde a las sucesiones con límite finito. Podemos decir que converge a '0' o a '1'.

• La sucesión an = 1/n converge a 0. Por ejemplo:

1, 1/2, 1/3, 1/4, 1/5..., 1/n

• La sucesión an = n/n+1 converge a 1.Por ejemplo:

1/2, 2/3, 3/4, 4/5, ..., n/n+1

2. Sucesiones divergentes

Este tipo de sucesión algebraica es de límite infinito. Se representa con el símbolo del infinito (∞) o tres puntos suspensivos.

• La fórmula es 2n+3, por ejemplo:

5, 7, 9, 11, 13, 2n+3

3. Sucesiones oscilantes

Estas sucesiones no son ni convergentes, ni divergentes, se alterna de mayor a menor y viceversa. Por ejemplo:

1, 0, 3, 0, 5, 0, 7, ...

InicioÁlgebra

¿Cuántos tipos de sucesiones existen en el álgebra?

Sucesiones

• ¿Qué es el límite de una sucesión?
• ¿Cuántos tipos de sucesiones existen en el álgebra?
• ¿Sucesión y progresión aritmética es lo mismo?

Aunque todas las sucesiones matemáticas sean conjuntos de elementos dispuestos de forma ordenada, existen diversos tipos de sucesiones que debes conocer. La clasificación de las sucesiones depende, entre otros factores, de la disposición de los elementos en la sucesión y del límite de la sucesión en sí. ¿Quieres saber cuántos tipos de sucesiones existen en el álgebra? Presta especial atención.

Clases de sucesiones algebraicas

Una sucesión (an) es un grupo de elementos, normalmente números, que están colocados de forma ordenada siguiendo una aplicación lógica. Estas aplicaciones pueden ser incontables, pero se pueden agrupar en diferentes tipos de sucesiones según cómo esté formado el conjunto y del límite de términos que pueda contener.

En primer lugar todas las sucesiones pueden ser finita o infinita,a partir de esta primera clasificación, se van definiendo el resto:

• Sucesión finita: es una sucesión, una serie de elementos que tienen un final. El primer y último número ya están definidos.
• Sucesión infinita: son aquellas sucesiones que no tienen un final y siempre se distinguen por ir seguido de los tres puntos (...).

Una vez entendida esta clasificación de sucesiones algebraicas más general, profundizamos en los distintos tipos de sucesiones matemáticas definiendo cada una:

1. Sucesiones convergentes

Este tipo corresponde a las sucesiones con límite finito. Podemos decir que converge a '0' o a '1'.

• La sucesión an = 1/n converge a 0. Por ejemplo:

1, 1/2, 1/3, 1/4, 1/5..., 1/n

• La sucesión an = n/n+1 converge a 1.Por ejemplo:

1/2, 2/3, 3/4, 4/5, ..., n/n+1

2. Sucesiones divergentes

Este tipo de sucesión algebraica es de límite infinito. Se representa con el símbolo del infinito (∞) o tres puntos suspensivos.

• La fórmula es 2n+3, por ejemplo:

5, 7, 9, 11, 13, 2n+3

3. Sucesiones oscilantes

Estas sucesiones no son ni convergentes, ni divergentes, se alterna de mayor a menor y viceversa. Por ejemplo:

1, 0, 3, 0, 5, 0, 7, ...

4. Sucesiones alternadas

Estas sucesiones hacen a su vez otra clasificación de sucesiones numéricas- convergentes, divergentes y oscilantes- y son aquellas que alternan los signos de sus términos o números.

• Sucesiones alternadas convergentes: Son aquellas que tienen límite=0 sean pares o impares.

1, −1, 0.5, −0.5, 0.25, −0.25, 0.125, −0.125,..

• Sucesiones alternadas divergentes: cuando tanto términos pares o impares su límite=∞.

1, 1, 2, 4, 3, 9, 4, 16, 5, 25, ...

• Sucesiones alternadas oscilantes: son las series en las que se cumple la siguiente fórmula: (−1)n n

−1, 2, −3, 4 ,−5, ..., (−1)n n

5. Sucesiones monótonas

Las sucesiones monótonas se clasifican en sucesiones monótonas crecientes y decrecientes. Por tanto, estas serie numéricas se dan cuando los términos de la sucesión crecen y decrecen. Crecientes sería cuando cada uno de los números es igual o menor que el que le sigue. Y. decreciente lo contrario, cuando los números son mayores o iguales que el siguiente.

Creciente: ann < ó = an +1

Decreciente: an > ó = an+ 1

6. Sucesiones acotadas

Se dice que es una sucesión acotada cuando la serie ha de estar comprendida entre dos número definidos, llamemos los 'k' y 'K'. Existen dos tipos de sucesiones acotadas en álgebra según el número que limita la secuencia:

• Secuencia acotada superiormente: Se define cuando todos los númros son iguales o mayores a un número La fórmula es :

an ≤ K.

• Secuencia acotada inferiormente: Cuando todos los términos son iguales o menores a un número K. Este número se nombra como cota inferior.

k ≤ an ≤ K

Si, como ocurre en el ejemplo, la sucesión no tiene términos iguales, se dice que es una sucesión estrictamente creciente. Se dice que una sucesión de números reales es monótona decreciente si cada término es mayor o igual que el siguiente. Es decir los términos van disminuyendo su valor o, a lo sumo, son iguales. 

¿Que es?

El dominio de una función f ( x ) es el conjunto de todos los valores para los cuales la función está definida, y el rangode la función es el conjunto de todos los valores que f toma. (En gramática, probablemente le llame al dominio el conjunto reemplazo y al rango el conjunto solución. 

EJERCICIOS

EJERCICIO 1: Determinar Dominio y Rango de f(x) = X + 3 

EJERCICIO 2 : Determinar Dominio y Rango de f(x) = x2 - 2x - 3

EJERCICIO 3: Determinar Dominio y Rango de f(x) = - x2 + 5x - 4

EJERCICIO 4 : Determinar Dominio y Rango de f(x) = x3 - 6x2 + 8x